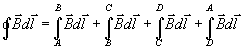La ley de Ampère

Campo magnético producido por una corriente rectilínea

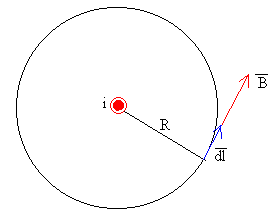La dirección del campo en un punto P, es perpendicular al plano determinado por la corriente y el punto.   Elegimos como camino cerrado una circunferencia de radio r, centrada en la corriente rectilínea, y situada en una plano perpendicular a la misma.

• El campo magnético B es tangente a la circunferencia de radio r, paralelo al vector dl.

• El módulo del campo magnético B tiene tiene el mismo valor en todos los puntos de dicha circunferencia.

La circulación (el primer miembro de la ley de Ampère) vale

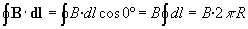
3. La corriente rectilínea i atraviesa la circunferencia de radio r.
    

4. Despejamos el módulo del campo magnético B.

Llegamos a la expresión obtenida aplicando la ley de Biot. 

Podemos generalizar este resultado para establecer la ley de Ampere:

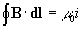
La ley de Gauss nos permitía calcular el campo eléctrico producido por una distribución de cargas cuando estas tenían simetría (esférica, cilíndrica o un plano cargado).

Del mismo modo la ley de Ampère nos permitirá calcular el campo magnético producido por una distribución de corrientes cuando tienen cierta simetría.

Los pasos que hay que seguir para aplicar la ley de Ampère son similares a los de la ley de Gauss.

1. Dada la distribución de corrientes deducir la dirección y sentido del campo magnético

2. Elegir un camino cerrado apropiado, atravesado por corrientes y calcular la circulación del campo magnético.

3. Determinar la intensidad de la corriente que atraviesa el camino cerrado

4. Aplicar la ley de Ampère y despejar el módulo del campo magnético.

Solenoide

Si suponemos que el solenoide es muy largo y estrecho, el campo es aproximadamente uniforme y paralelo al eje en el interior del solenoide, y es nulo fuera del solenoide. En esta aproximación es aplicable la ley de Ampère.

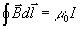
El primer miembro, es la circulación del campo magnético a lo largo de un camino cerrado, y en el segundo miembro el término I se refiere a la intensidad que atraviesa dicho camino cerrado.

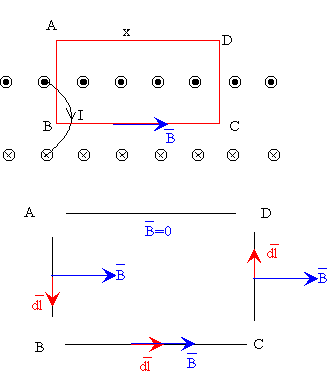
Para determinar el campo magnético, aplicando la ley de Ampère, tomamos un camino cerrado ABCD que sea atravesado por corrientes. La circulación es la suma de cuatro contribuciones, una por cada lado.

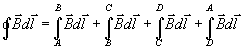
Examinaremos, ahora cada una de las contribuciones a la circulación:

1. Como vemos en la figura la contribución a la circulación del lado AB es cero ya que bien 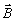y 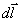son perpendiculares, o bien 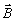es nulo en el exterior del solenoide.

2. Lo mismo ocurre en el lado CD.

3. En el lado DA la contribución es cero, ya que el campo en el exterior al solenoide es cero.

4. En el lado BC, el campo es constante y paralelo al lado, la contribución a la circulación es Bx, siendo x la longitud del lado.

La corriente que atraviesa el camino cerrado ABCD se puede calcular fácilmente:

Si hay N espiras en la longitud L del solenoide en la longitud x habrá Nx/L espiras por las que circula una intensidad I. Por tanto, la ley de Ampère se escribe para el solenoide.

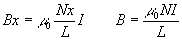
Este es el ejemplo que muestra la dirección http://physics.rug.ac.be/fysica/applets/MagnetischVeld1/